J.C. Tchang
On Michael Heidemann Site
| J.C. Tchang |
Original Version On Michael Heidemann Site |
L'utilitaire Inliner vous permet de décomposer, dans un fichier LDraw, les primitives et parties de pièces (lignes de type 1), en leurs composants, de façon récursive.
C'est une simple application utilisant la console DOS, aidant les créateurs de pièces LDraw.
Voici une copie d'écran d'un exemple d'exécution :
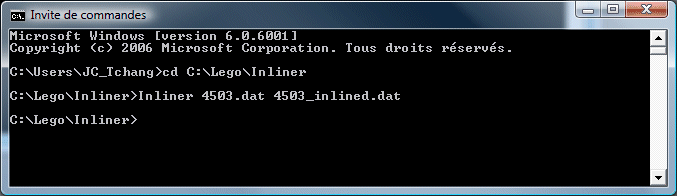
Il est possible de lancer Inliner à partir d'une interface
plus conviviale que la ligne de commande. LETGUI crée par Michael Heidemann
est fait pour cela.
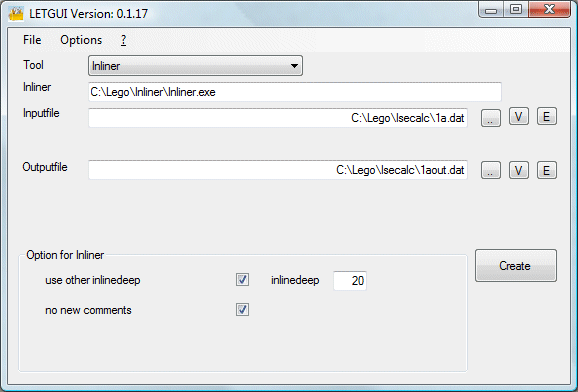
 . Ce fichier
peut être visualisé en cliquant sur le bouton
. Ce fichier
peut être visualisé en cliquant sur le bouton  , ou
édité avec le bouton
, ou
édité avec le bouton 
 .
.
Pour plus d'informations générales sur cette interface, allez sur la page LETGUI.
Si vous avez fait, par exemple, une primitive avec le mauvais sens des faces, il est possible d'utiliser Inliner pour retourner toutes les faces :
Nota : Origine de ce chapitre sur le site http://news.lugnet.com/ message 16020.
Il y a plusieurs choses à faire attention, lorsque l'on veut substituer le contenu d'un sous-fichier à la ligne l'appelant dans le fichier parent.
Le premier problème est de modifier toutes les lignes du sous-fichier, car la position des entités dans ce sous-fichier est dans un référentiel x, y, z, alors que dans le fichier parent il est dans un autre référentiel x1, y1, z1. Ces référentiels ont généralement une origine différente, mais également une orientation différente. Le chapitre 1 vous explique comment faire, en passant par une matrice de transformation.
Le second problème, est de faire attention au sens des faces pour les triangles et les quadrilatères. Le chapitre 2 vous explique comment faire.
Comment calculer les lignes insérées avec sa position et sa matrice de transformation ?
Chaque ligne de type 1 à le format suivant :
1 <colour> x y z a b c d e f g h i <subfile>
Où x y z définit l'origine de l'élément et a...i la matrice de transformation. Avec ces informations, nous pouvons créer une matrice 4 x 4 qui ressemble à ceci :
| a d g 0 | | b e h 0 | | c f i 0 | | x y z 1 |
Cette matrice est la base pour les calculs suivants.
Chaque sous-fichier peut contenir des lignes de type 1, 2, 3, 4 et 5, qui devront être recalculées.
Il s'agit d'une commande d'appel du sous-fichier <subfile>
1 <colour> x1 y1 z1 a1 b1 c1 d1 e1 f1 g1 h1 i1 <subfile>
En correspondance avec la matrice précédente, nous pouvons construire la matrice de cette ligne :
| a1 d1 g1 0 | | b1 e1 h1 0 | | c1 f1 i1 0 | | x1 y1 z1 1 |
Les nouveaux paramètres de la matrice sont calculés comme suit :
a1 = a*a1 + b*d1 + c*g1 + x*0
d1 = d*a1 + e*d1 + f*g1 + y*0
g1 = g*a1 + h*d1 + i*g1 + z*0
b1 = a*b1 + b*e1 + c*h1 + x*0
c1 = a*c1 + b*f1 + c*i1 + x*0
x1 = a*x1 + b*y1 + c*z1 + x*1
e1 = d*b1 + e*e1 + f*h1 + y*0
f1 = d*c1 + e*f1 + f*i1 + y*0
y1 = d*x1 + e*y1 + f*z1 + y*1
h1 = g*b1 + h*e1 + i*h1 + z*0
i1 = g*c1 + h*f1 + i*i1 + z*0
z1 = g*x1 + h*y1 + i*z1 + z*1
Il s'agit d'une commande de création d'une ligne définie par 2 points.
2 <colour> x1 y1 z1 x2 y2 z2
Les coordonnées des nouveaux points sont calculées comme suit :
x1 = a*x1 + d*y1 + g*z1 + x
x2 = a*x2 + d*y2 + g*z2 + x
y1 = b*x1 + e*y1 + h*z1 + y
z1 = c*x1 + f*y1 + i*z1 + z
y2 = b*x2 + e*y2 + h*z2 + y
z2 = c*x2 + f*y2 + i*z2 + z
Il s'agit d'une commande de création d'une face en forme de triangle définie par 3 points.
3 <colour> x1 y1 z1 x2 y2 z2 x3 y3 z3
Les coordonnées des nouveaux points sont calculées comme suit :
x1 = a*x1 + d*y1 + g*z1 + x
x2 = a*x2 + d*y2 + g*z2 + x
x3 = a*x3 + d*y3 + g*z3 + x
y1 = b*x1 + e*y1 + h*z1 + y
z1 = c*x1 + f*y1 + i*z1 + z
y2 = b*x2 + e*y2 + h*z2 + y
z2 = c*x2 + f*y2 + i*z2 + z
y3 = b*x3 + e*y3 + h*z3 + y
z3 = c*x3 + f*y3 + i*z3 + z
Il s'agit d'une commande de création d'une face en forme de quadrilatère définie par 4 points.
4 <colour> x1 y1 z1 x2 y2 z2 x3 y3 z3 x4 y4 z4
Les coordonnées des nouveaux points sont calculées comme suit :
x1 = a*x1 + d*y1 + g*z1 + x
x2 = a*x2 + d*y2 + g*z2 + x
x3 = a*x3 + d*y3 + g*z3 + x
x4 = a*x4 + d*y4 + g*z4 + x
y1 = b*x1 + e*y1 + h*z1 + y
z1 = c*x1 + f*y1 + i*z1 + z
y2 = b*x2 + e*y2 + h*z2 + y
z2 = c*x2 + f*y2 + i*z2 + z
y3 = b*x3 + e*y3 + h*z3 + y
z3 = c*x3 + f*y3 + i*z3 + z
y4 = b*x4 + e*y4 + h*z4 + y
z4 = c*x4 + f*y4 + i*z4 + z
Il s'agit d'une commande de création d'une ligne conditionnelle définie par 4 points.
5 <colour> x1 y1 z1 x2 y2 z2 x3 y3 z3 x4 y4 z4
Comme vous pouvez le voir, le format de la ligne est similaire au type de ligne 4, et en conséquence, les coordonnées se calculent de façon identique.
Comment vérifier l'information du bon sens des faces dans les sous-fichiers à décomposer ?
Il y a 3 informations que vous devez prendre en compte pour résoudre cela.
Chaque fichier ou sous-fichier doit avoir une ligne "0 BFC CERTIFY CCW", ou "0 BFC CERTIFY CW". Si tous les fichiers (sous-fichiers, et fichier parent) ont le même sens des faces, alors il n'y a rien à faire, mais si c'est différent, vous devez changer le sens des triangles et quadrilatères.
Si la ligne de commande qui précède la ligne de type 1 est "0 BFC INVERTNEXT", alors vous devez changer le sens des triangles et quadrilatères.
S'il vous plait, ne me demandez pas qu'est-ce qu'un déterminant, car la seule chose que j'ai compris sur cela, est ce qui concerne la direction du sous-fichier. Si le déterminant est négatif, alors vous devez changer le sens des triangles et quadrilatères.
Le déterminant est calculé à partir d'une partie de la matrice de transformation de la ligne du sous-fichier :
1 <colour> x y z a b c d e f g h i <file>
| a d g | | b e h | => Déterminant = a*e*i + d*h*c + g*b*f - a*h*f - d*b*i - g*e*c | c f i |
Tout ceci peut être mis dans un tableau, pour visualiser par OUI ou par NON, les 6 cas de figures, et si le résultat doit-être changé de sens ou non.
| Sens BFC différent ? | OUI | NON | NON | NON | OUI | OUI |
|---|---|---|---|---|---|---|
| BFC Invertnext ? | OUI | OUI | NON | NON | NON | OUI |
| Déterminent négatif ? | OUI | OUI | OUI | NON | NON | NON |
| Alors, changer le sens ? | OUI | NON | OUI | NON | OUI | NON |
Un triangle est défini par 3 points, et si vous inversez 2 de ces points, vous changez le sens du triangle.
Ligne de commande originale :
3 <colour> x1 y1 z1 x2 y2 z2 x3 y3 z3
Ligne de commande avec le triangle inversé :
3 <colour> x3 y3 z3 x2 y2 z2 x1 y1 z1
Un quadrilatère est défini par 4 points, et vous devez inverser l'ordre de ces points, pour changer son sens.
Ligne de commande originale :
4 <colour> x1 y1 z1 x2 y2 z2 x3 y3 z3 x4 y4 z4
Ligne de commande avec le quadrilatère inversé :
4 <colour> x4 y4 z4 x3 y3 z3 x2 y2 z2 x1 y1 z1
Le programme Inliner et son manuel d'utilisation appartiennent à (c) Michael Heidemann (mikeheide). Pour plus d'information sur les droits, lisez son fichier "Lizenz.txt" fourni avec le programme.
La compilation des informations sur la théorie matricielle, et le sens des faces, a été fait également par (c) Michael Heidemann (mikeheide) au 28-06-2006. Les corrections sont bienvenues.
Vous pouvez le retrouver sur son site et sa page d'accueil, et sur les versions d'origine en anglais de cette page.
Traduction et Adaptation : J.C. Tchang.