J.C. Tchang
| J.C. Tchang |
Voici un petit tutoriel pour mieux maitriser la déformation de primitives dans la création de pièces LDraw.

Sur l'image ci-dessus, la primitive "box2-5.dat" de base, en jaune, a été "déformée" pour obtenir la figure en vert. Il s'agit de la même primitive, en modifiant uniquement la matrice de transformation.
Personnellement pour faire mes pièces, j'utilise le programme MLCad, pour
tout ce qui est création générale, positionnement et orientation.
Pour les déformations et orientations particulières, j'utilise le couple de
programmes LDDP et LDView, qui permettent de tester en interactif
le changement de valeur.
En jonglant avec ces 3 programmes on arrive à trouver les bonnes valeurs, sans trop
approfondir la théorie.
Exemple :
1 9 0 0 0 1 0 0 0 1 0 0 0 1 rect.datDescription générale d'une ligne de commande de primitive :
Le résultat à l'affichage dépend de la valeur, de son signe, et du choix d'un paramètre dans chaque triplet pour la dimension et l'orientation orthogonale. Pour une orientation quelconque 2 ou 3 paramètres de chaque triplet est affecté.
Chaque triplet peut être décomposé en paramètres X, Y, et Z du triplet.
La position de la valeur de dimension dans chaque triplet varie en fonction de l'orientation orthogonale de la primitive. Si la primitive est orientée d'une valeur quelconque dans l'espace, alors l'ensemble du triplet est modifié, et nous sortons du cadre de ce tutoriel. Pour une information plus complète, voir la théorie sur la décomposition des lignes de type 1, dans la page consacrée à Inliner.
Pour les primitives planes la valeur de la matrice correspondant au plan (Y par défaut) devait être égal à 1, mais depuis 12-2015 cette valeur doit seulement être différente de 0.
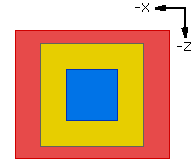 |
1 9 0 0 0 1 0 0 0 1 0 0 0 1 rect.datLigne de commande rect.dat : Commence par 1 pour primitive, 9 pour couleur bleu, puis en vert les paramètres de position X, Y et Z, et en bleu les 9 paramètres de dimension et orientation (3 en X, 3 en Y et 3 en Z). Par défaut, dans le plan XZ, nous avons une face carrée (en bleu sur l'image) de 1x1 LDU (LDraw Unit). 1 14 0 0 0 2 0 0 0 1 0 0 0 2 rect.datSi nous mettons une valeur identique en X et Z (ici 2) nous obtenons une face carrée de 2x2 LDU (en jaune sur l'image). 1 12 0 0 0 3 0 0 0 1 0 0 0 2.5 rect.datSi nous mettons une valeur différente en X et Z (ici 3 et 2.5) nous obtenons une face rectangulaire de 3x2.5 LDU (en rouge sur l'image). Depuis 12-2015, la valeur en Y (ici 1) peut avoir une valeur quelconque mais non nulle. |
La primitive rect comporte par défaut les 4 bords de la face (ou cotés du carré). Vous pouvez utiliser les autres primitives "rect", comme rect1, rect2a, rect2p, ou rect3 si vous n'avez pas besoin de tous les bords.
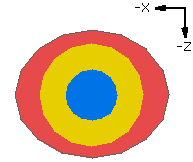 |
1 9 0 0 0 1 0 0 0 1 0 0 0 1 4-4disc.datLigne de commande 4-4disc.dat : Commence par 1 pour primitive, 9 pour couleur bleu, puis en vert les paramètres de position X, Y et Z, et en bleu les 9 paramètres de dimension et orientation (3 en X, 3 en Y et 3 en Z). Par défaut, dans le plan XZ, nous avons une face circulaire (en bleu sur l'image) de 1x1 LDU (LDraw Unit). 1 14 0 0 0 2 0 0 0 1 0 0 0 2 4-4disc.datSi nous mettons une valeur identique en X et Z (ici 2) nous obtenons une face circulaire facettisée de 2x2 LDU (en jaune sur l'image). 1 12 0 0 0 3 0 0 0 1 0 0 0 2.5 4-4disc.datSi nous mettons une valeur différente en X et Z (ici 3 et 2.5) nous obtenons une face elliptique facettisée de 3x2.5 LDU (en rouge sur l'image). 1 0 0 0 0 3 0 0 0 1 0 0 0 2.5 4-4edge.datDepuis 12-2015, la valeur en Y (ici 1) peut avoir une valeur quelconque mais non nulle. Bien entendu la même chose est utilisée pour les bords avec la primitive edge (à l'extérieur en noir sur l'image). |
La primitive disc ne comporte par défaut aucun bord. Il faut utiliser la primitive edge pour cela. Nous avons utilisé ici les primitives complètes 4-4disc et 4-4edge. Vous pouvez utiliser les autres primitives donnant une portion de la face, comme 1-8disc, 1-4disc, 3-8disc, etc...
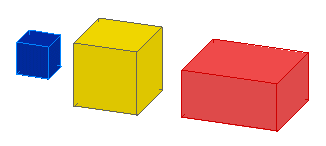 |
1 9 0 0 0 1 0 0 0 1 0 0 0 1 box.datPar défaut la primitive "box.dat" forme un cube de 2x2x2 LDU, pour une valeur 1 en X, Y et Z (en bleu sur l'image). 1 14 5 0 0 2 0 0 0 2 0 0 0 2 box.datSi nous mettons une valeur identique en X, Y et Z (ici 2) nous obtenons un cube de 4x4x4 LDU (en jaune sur l'image). 1 12 13 0 0 3 0 0 0 1.5 0 0 0 2.5 box.datSi nous mettons une valeur différente en X, Y et Z (ici 3 en X, 1.5 en Y et 2.5 en Z) nous obtenons un parallélépipède rectangle (en rouge sur l'image). |
Bien entendu, toutes les primitives "Box" partielles, c'est-à-dire les Primitives rectilignes à trois dimensions peuvent être utilisées.
 |
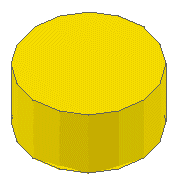
1 9 0 0 0 1 0 0 0 1 0 0 0 1 4-4cyli.datPar défaut la primitive "4-4cyli.dat" forme un tube cylindrique de 1 LDU de rayon, et 1 LDU de hauteur, pour une valeur 1 en X, Y et Z (en bleu sur l'image). 1 14 5 0 0 2 0 0 0 2 0 0 0 2 4-4cyli.datSi nous mettons une valeur identique en X, Y et Z (ici 2) nous obtenons un tube cylindrique de 4 LDU de diamètre pour 2 LDU de haut (en jaune sur l'image). 1 12 13 0 0 3 0 0 0 0.5 0 0 0 2.5 4-4cyli.datSi nous mettons une valeur différente aux axes du plan de base (ici 3 en X et 2.5 en Z) nous obtenons un tube elliptique (en rouge sur l'image) de hauteur Y (ici 0.5 LDU). |
La primitive cyli ne comporte par défaut ni bord ni fond. Il faut utiliser les primitives edge et disc pour cela. Nous avons utilisé ici les primitives complètes 4-4cyli. Vous pouvez utiliser les autres primitives donnant une portion de cylindre, comme 1-8cyli, 1-4cyli, 3-8cyli, etc...
Un cylindre est un tube cylindrique, fermé aux 2 extrémités.
 |
1 14 0 0 0 2 0 0 0 2 0 0 0 2 4-4cyli.dat 1 14 0 0 0 2 0 0 0 2 0 0 0 2 4-4edge.dat 1 14 0 0 0 2 0 0 0 2 0 0 0 2 4-4disc.dat 1 14 0 2 0 2 0 0 0 2 0 0 0 2 4-4edge.dat 1 14 0 2 0 2 0 0 0 2 0 0 0 2 4-4disc.dat |
Pour obtenir un cylindre complet, il faut 5 primitives.
Vous pouvez remarquer que les 3 premières ont les mêmes paramètres, et les 2 suivantes,
ne diffèrent que par leur position suivant l'axe du cylindre (ici 2 en Y marqué en rouge, comme la valeur Y
de dimension de la première ligne).
Nota : Les valeurs 2 en bleu pour les primitives "disc" et "edge" sont là car ces primitives ont été
créées par copie des valeurs de la primitive "cyli". Cette valeur devrait être "1" par défaut (plus depuis 12-2015), mais
cela ne change pas l'affichage. Par contre cette valeur ne doit pas être nulle. De même
ce mode de création ne tient pas compte du sens des faces que l'on peut trouver en ajoutant
un signe "-" bien placé (voir plus bas avec la fermeture de tube tronqué).
Bien sûr, toutes les combinaisons sont possibles avec les portions de cylindres.
Nota : Pour information, il existe une primitive de cylindre complet : rod.dat.
 |
1 9 0 0 0 1 0 0 0 1 0 0 0 1 4-4cyls.dat 1 14 3 0 0 1 0 0 0 3 0 0 0 1 4-4cyls.dat |
Cette primitive, montrée ici en plan, permet de créer des tubes cylindriques tronqués, ou en sifflet. En modifiant la valeur en Y (en orientation par défaut), on change la longueur du tube. En changeant les valeurs en X et Z, on change le rayon du tube. Si les valeurs X, Y, et Z sont identiques, l'angle du sifflet est de 45°.
Comme pour les tubes plus haut, cette primitive ne comporte ni bords ni fonds, mais est apparu depuis une primitive 4-4cylse.dat comportant le tube tronqué + le bord incliné.
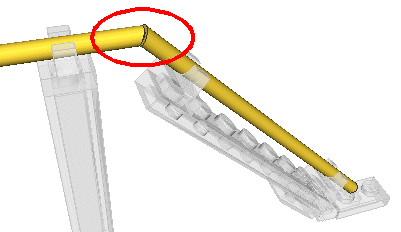
Voir un usage de tubes tronqués dans :
Tuyau de guidage avec extrémité coupé en sifflet.
Les primitives "rect" peuvent être déformées en forme de parallélogramme et en forme
de losange.
Nota : Il n'est pas possible avec les primitives LDraw de déformer un rectangle en trapèze,
car dans tous les cas les bords parallèles restent parallèles.
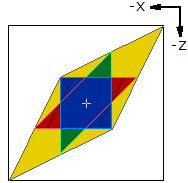 |
Voici une superposition de primitives rect.dat permettant de visualiser différentes déformations planes. |
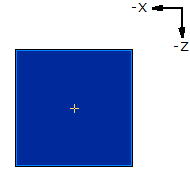 |
1 9 0 0 0 1 0 0 0 1 0 0 0 1 rect.datA partir d'une primitive de base. |
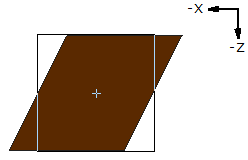 |
1 6 0 0 0 1 0 0.5 0 1 0 0 0 1 rect.datEn changeant la valeur Z de la direction X, on déforme en parallélogramme. Nota : Cette technique est également employée plus bas pour Mettre un texte en italique. |
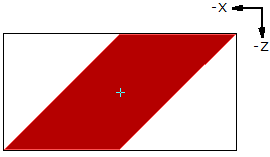 |
1 4 0 0 0 1 0 1 0 1 0 0 0 1 rect.datEn mettant la même valeur au premier et au troisième paramètre de la matrice de transformation on obtient un angle de 45°. |
 |
1 2 0 0 0 1 0 0 0 1 0 1 0 1 rect.datEn changeant la valeur X de la direction Z, on déforme en parallélogramme dans l'autre direction. |
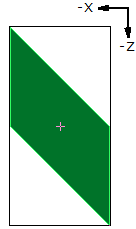 |
1 2 0 0 0 1 0 0 0 1 0 -1 0 1 rect.datSi la valeur est négative, la déformation va en Z négatif. |
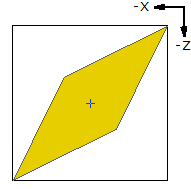 |
1 14 0 0 0 1 0 2 0 1 0 2 0 1 rect.datEn changeant la valeur suivant les 2 directions, on déforme en losange incliné. Voir également plus bas le chapitre sur La "diagonale du fou". |
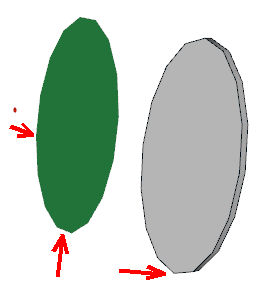 |
Voici une solution pour avoir le sommet plat sur un disque déformé (en vert).
Habituellement un disc déformé a les sommets pointus (ici en gris à droite, un disque faisant 20 LDU en X et 38.6 LDU en Y,
utilisé sur la pièce 92747.dat). 1 16 0 0 -8 20 0 0 0 0 38.6 0 1 0 4-4disc.dat
Pour avoir un plat au sommet, créer un disque unitaire de 1 LDU, ici à gauche en rouge, et le faire tourner avec MLCad de 11.25° (360/32)
autour de l'axe Z. Ci-dessous les paramètres de la matrice X en bleu, et Y en rouge. 1 4 -80 0 -8 0.980785 0 -0.19509 0.19509 0 0.980785 0 1 0 4-4disc.dat
Pour obtenir le résultat, il suffit de multiplier les différentes valeurs non nulles de la matrice X par 20,
et les valeurs de la matrice Y par 38.6. 1 2 -50 0 -8 19.6157 0 -3.9018 7.53047 0 37.8583 0 1 0 4-4disc.dat |
La fermeture à la base est identique à la fermeture du cylindre. Pour l'autre extrémité tronquée, il faut jouer avec une déformation 3D d'un disque (disc) et d'un bord (edge).
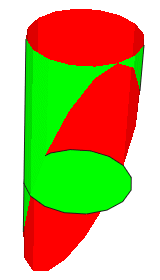 |
1 14 0 0 0 1 0 0 0 3 0 0 0 1 4-4cyls.dat 1 13 0 3 0 1 0 0 0 1 0 0 0 1 4-4disc.dat 1 13 0 3 0 1 0 0 0 1 0 0 0 1 4-4edge.datLa primitive "cyls" a une hauteur de 3 LDU en Y. Les 2 primitives "disc" et "edge" sont placés à Y=3 dans cet exemple, c'est-à-dire au milieu de la face tronquée. |
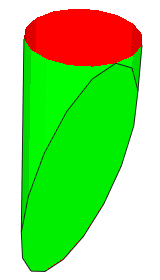 |
1 13 0 3 0 1 0 0 -3 -1 0 0 0 1 4-4disc.dat 1 13 0 3 0 1 0 0 -3 1 0 0 0 1 4-4edge.datLes 2 primitives "disc" et "edge" précédentes sont déformées d'une valeur -3 en Y pour obtenir la fermeture de l'extrémité tronquée. Nota : Le signe négatif est la pour obtenir la bonne orientation. La valeur -1 sur la primitive "disc" est la pour obtenir le bon coté de la face sur l'extérieur (sinon elle serait montrée en rouge sur l'image à gauche, sur un test "BFC" dans LDView. |
Par déformation de tube tronqué, on peut raccorder 2 tubes perpendiculaires.
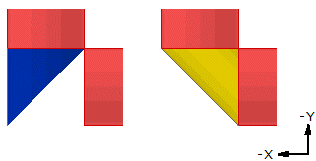
|
Primitives des cylindres et bords de base, vus dans le plan XY :
1 12 0 -1 0 1 0 0 0 1 0 0 0 1 4-4cyli.dat 1 12 1 1 0 0 1 0 -1 0 0 0 0 1 4-4cyli.dat 1 12 0 0 0 1 0 0 0 1 0 0 0 1 4-4edge.dat 1 12 1 1 0 0 1 0 -1 0 0 0 0 1 4-4edge.datPrimitive du cylindre coupé avant (en bleu) et après (en jaune) déformation : 1 1 0 0 0 1 0 0 0 1 0 0 0 1 4-4cyls.dat 1 14 0 0 0 1 1 0 0 1 0 0 0 1 4-4cyls.datNota : Attention, si la primitive "cyls" en jaune à ses 2 extrémités de forme circulaire, la section du tube (à 45°) n'est pas circulaire. Cette déformation peut être utile pour raccorder un demi-tube ou quart de tube sur un plan. Elle est montrée ici entre 2 tubes pour faciliter la démonstration de la "déformation" appliquée. Dans le cas d'un raccordement réel de 2 tubes, il est préférable de raccorder avec 1/4 de tore. |
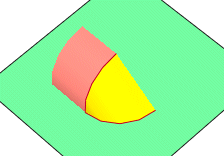 |
1 1 0 0 0 1 0 0 0 1 0 0 0 1 1-4cyls2.dat 1 14 0 0 0 1 1 0 0 1 0 0 0 1 1-4cyls2.datVoici avec la primitive "1-4cyls2" le raccordement de 1/4 de tube sur un plan. Nota : on peut obtenir l'autre partie par symétrie. |
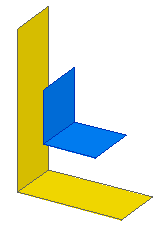 |
1 9 0 0 0 1 0 0 0 1 0 0 0 1 box2-5.dat 1 14 0 0 0 1 0 0 0 3 0 0 0 2 box2-5.datLa primitive "box2-5" forme 2 cotés d'une boite rectangulaire. Changer les paramètres de dimension pour en changer la taille (ici en Y et Z). |
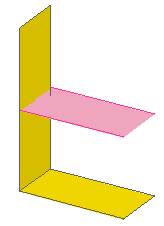 |
1 13 0 0 0 0 0 -1 0 1 0 2 0 0 rect2p.datInsertion d'une primitive "rect2p" qui ne comporte que 2 bords : Les paramètres de dimension et orientation sont ajustés avec MLCad pour obtenir les bonnes valeurs dans la bonne direction. Nota : La primitive est placée (ici à 0, 0, 0) pour être à mi-hauteur, et mi-largeur de la primitive en L. |
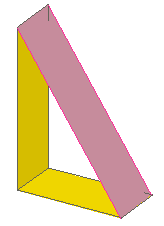 |
1 13 0 0 0 0 0 -1 -3 1 0 2 0 0 rect2p.datPar déformation en Y on obtient la fermeture du L. Nota : Il faut parfois jongler avec le signe et le bon paramètre (entre le 4ème et 6ème paramètre valant 0 pour les Y) pour obtenir la bonne face. |
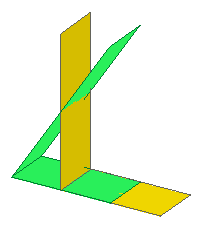 |
1 14 0 0 0 1 0 0 0 3 0 0 0 2 box2-5.dat 1 10 0 0 0 1 0 0 0 3 0 0 2 2 box2-5.datPar déformation en Z on obtient un L déformé. Ici, en vert, la déformation est d'une valeur 2 correspondant à la dimension en Z, ce qui permet par exemple de raccorder cette forme sur une face verticale. Voir comme exemple la pièce |
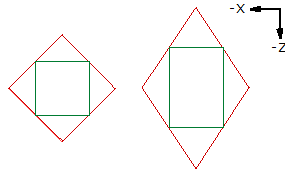 |
Comme on le voit sur ces exemples la déformation peut former une diagonale. Dans ces exemples la primitive (verte) est déformée pour obtenir un losange (saumon). On peut voir que ce n'est pas une déformation isométrique (à dimensions égales). |
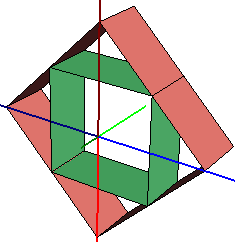 |
1 10 0 0 0 0 0 1 0 1 0 -1 0 0 box4.dat 1 12 0 0 0 1 0 1 0 1 0 -1 0 1 box4.datInsertion d'une primitive box4 standard, avec la même dimension en X et Z, formant un carré. Par déformation en X et Z de la dimension en X et Z on obtient une forme de losange d'une dimension égale à la diagonale du carré de base. |
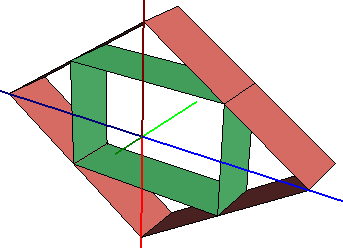 |
1 10 0 0 0 0 0 1 0 1 0 -1.5 0 0 box4.dat 1 12 0 0 0 1 0 1 0 1 0 -1.5 0 1.5 box4.datInsertion d'une primitive box4 standard, avec une dimension différente en X et Z, formant un rectangle. Par déformation en X et Z de la dimension en X et Z on obtient une forme de losange d'une dimension égale à la diagonale du rectangle de base. Les angles ne sont plus à 90°. |
 |
Dans quel cas utiliser cette technique ? Lorsqu'il s'agit de mettre en place
une primitive qui n'est pas orientée suivant les axes, et dont on connait les dimensions
combinées suivant 2 axes et non la dimension de la diagonale qui est sur 1 axe.
Cela permet de garder des dimensions exactes (pas de facteur 1,4142135....)
et évite une rotation amenant également des arrondis. Dans l'exemple à gauche de la pièce 641.dat, que j'ai repris, la primitive box2-5.dat (mise en rouge) utilise cette technique. |
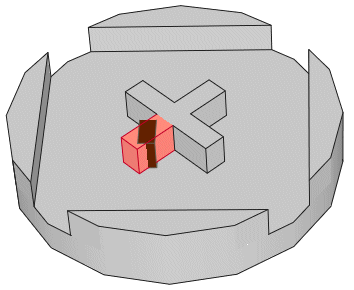 |
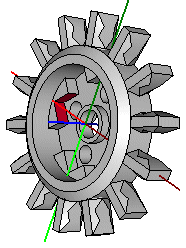
Nota : Retrouvée par hasard, la pièce 4150s01.dat, d'Andy Westrate, datant de 2003,
utilise cette technique pour la création de la partie en croix. La partie rose finale est obtenue par déformation de la primitive "box4-4a" marron. 1 6 -3 4 3 1 0 0 0 4 0 0 0 2 box4-4a.dat 1 12 -3 4 3 1 0 -2 0 4 0 1 0 2 box4-4a.dat |
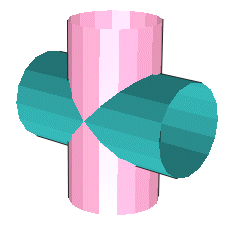 |
1 13 0 0 0 2 0 0 0 8 0 0 0 2 4-4cyli.dat 1 11 -4 4 0 0 8 0 -2 0 0 0 0 2 4-4cyli.dat Définition des 2 cylindres perpendiculaires. |
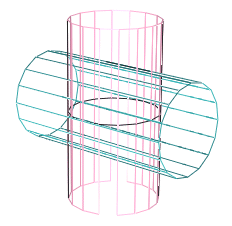 |
1 4 0 4 0 2 0 0 0 8 0 0 0 2 4-4edge.dat Définition d'un bord (edge) avec les mêmes paramètres de dimension et orientation que le premier cylindre. |
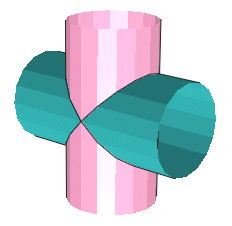 |
1 10 0 4 0 2 0 0 2 8 0 0 0 2 4-4edge.dat 1 10 0 4 0 2 0 0 -2 8 0 0 0 2 4-4edge.dat Copie et modification du bord précédent pour le déformer d'un rayon de 2, pour construire les 2 courbes d'intersection des cylindres. |
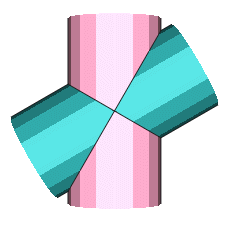 |
1 13 0 0 0 2 0 0 0 8 0 0 0 2 4-4cyli.dat 1 11 -3.463 6 0 -1 6.9282 0 -1.73205 -4 0 0 0 2 4-4cyli.dat 1 10 0 4 0 2 0 0 1.1547 8 0 0 0 2 4-4edge.dat 1 10 0 4 0 2 0 0 -3.4641 8 0 0 0 2 4-4edge.dat Ici, l'angle entre les 2 cylindres est de 30°, pour construire les 2 courbes d'intersection des cylindres, la méthode est la même, mais pour le calcul des valeurs il faut un peu de géométrie : |H1|= R x tg(angle), soit 2 x tg(30) = 1.1547. |H2|= H1 + R/cos(angle), soit 1.1547 + 2/cos(30) = 3.4641 Nota : Pour ceux qui ont des problèmes avec la géométrie, ils peuvent aussi trouver la valeur par approximation en modifiant les valeurs dans LDDP, et en regardant le résultat avec LDView :-). |
Nota : Pour utiliser les primitives edge en intersections de tubes, il est nécessaire que les 2 tubes soient de même diamètre, et coplanaires (leurs axes se croisent).
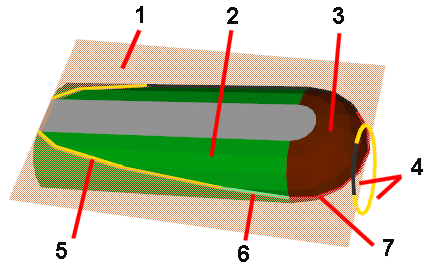
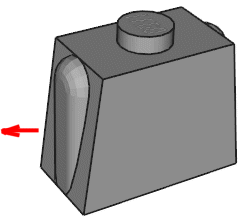
Dans l'exemple ci-dessus, basé sur la reprise du bras de la pièce 17.dat (Minifig Torso Old), Nous avons en 5 une primitive 3-16edge.dat déformée pour générer l'intersection de la portion de cylindre 2 par le plan 1.
Lignes de commandes de l'exemple :
0 // Plane
4 57 20 32 10 16 0 10 16 0 -10 20 32 -10
0 // Cylinder
1 2 16 6 2 4 0 0 0 26 0 0 0 4 1-4cyli.dat
0 // Tore (Cone)
1 6 16 6 0 0 2 0 0 0 -2 2 0 0 r04o2000.dat
0 // Unstretch Edge
1 24 16 0 2 4 0 0 0 1 0 0 0 4 4-4edge.dat
1 14 16 0 2 4 0 0 0 1 0 0 0 4 3-16edge.dat
0 // Stretch Edge
1 14 16 0 2 4 0 0 32 1 0 0 0 4 3-16edge.dat
0 // Lines
2 10 16.75 6 5.85 17.5308 12.2464 5.6956
2 4 16.4674 3.7393 5.4575 16.5698 4.5585 5.6001
2 4 16.5698 4.5585 5.6001 16.75 6 5.8509
2 4 16.2236 1.7888 4.2112 16.4674 3.7393 5.4575
2 4 16.2236 1.7888 4.2112 16.0584 0.4673 2.2918
2 4 16.0584 0.4673 2.2918 16 0 0
Nota : En rouge la seule valeur modifiée pour "déformer" la primitive 5 : 3-16edge.dat. Cette valeur de 32 correspond à la "hauteur" du plan : 1.
Nous allons essayer de placer un motif sur une face, sans calculer d'angle, mais en déformant ce motif, tout en le gardant plan.
 |
Pour cet exemple, nous allons utiliser le motif test_def_1.dat,
crée avec Quad2Dat.
Il fait 40x40 LDU en X et Z, et utilise des triangles, quadrilatères et primitives, elles-mêmes déformées (ovale). |
 |
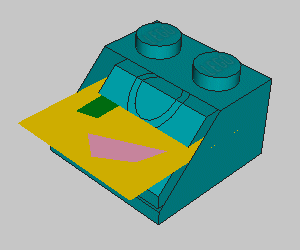
1 3 0 0 0 1 0 0 0 1 0 0 0 1 s\3039s01.dat 1 15 -50 10 -20 1 0 0 0 1 0 0 0 1 test_def_1.dat Ici, une "Slope 2x2" sans sa face inclinée, et notre motif placé à côté. |
 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 s\3039s01.dat 1 15 0 10 -20 1 0 0 0 1 0 0 0 1 test_def_1.dat Les mêmes éléments avec le centre du motif mis au centre de la face à remplir. Mais notre motif est trop grand en profondeur (en Z) ... |
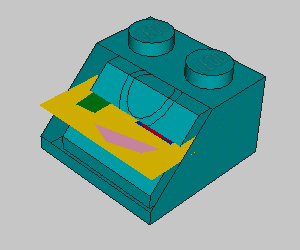 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 s\3039s01.dat 1 15 0 10 -20 1 0 0 0 1 0 0 0 0.5 test_def_1.dat La profondeur projetée en vue de dessus de la pente étant de 20 LDU (distance en Z des 2 lignes de bords horizontales), et le motif faisant 40 LDU, il suffit de mettre 0.5 au lieu de 1 en Z. |
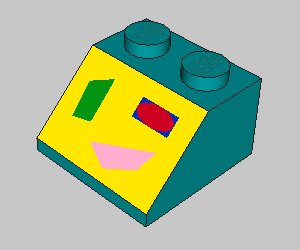 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 s\3039s01.dat 1 15 0 10 -20 1 0 0 0 1 -0.5 0 0 0.5 test_def_1.dat Et maintenant, surprise, par une simple "déformation", nous allons plaquer le motif sur la face : Il suffit de mettre une valeur au "bon endroit". Dans notre cas, nous voulons déformer en Y, avec une évolution suivant Z, c'est donc le 6ème paramètre de la matrice qu'il faut modifier. La valeur reprend la valeur de dimension en Z, c'est-à-dire le 9ème paramètre (ici 0.5). J'avoue que pour le signe, qui va donner la bonne direction, je teste, et je mets le signe "-" comme ici, quand la face est mal orientée. C'est terminé, le motif est bien placé, et rempli correctement la face. |
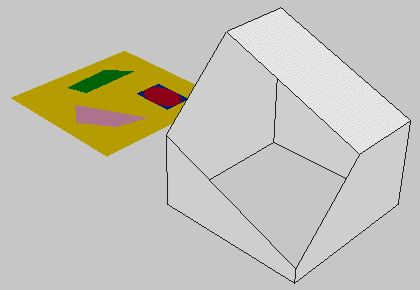 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 test_def_3a.dat 1 15 -50 10 -20 1 0 0 0 1 0 0 0 1 test_def_1.dat Ici, une pièce basée sur la pièce "Slope 2x2" dont la face inclinée manquante est inclinée suivant 2 directions, et notre motif placé à côté. |
 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 test_def_3a.dat 1 15 0 2 -20 1 0 0 0 1 0 0 0 1 test_def_1.dat Les mêmes éléments avec le centre du motif mis au centre de la face à remplir. Le centre est la moyenne en XYZ des extrêmes des lignes de bord en X, en Y, et en Z. |
 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 test_def_3a.dat 1 15 0 2 -20 1 0 0 0 1 0 0 0 0.5 test_def_1.dat De la même façon que dans l'exemple précédent, la profondeur projetée en vue de dessus de la pente étant de 20 LDU (distance en Z des 2 lignes de bords les plus horizontales), et le motif faisant 40 LDU, il suffit de mettre comme précédemment 0.5 au lieu de 1 en Z. |
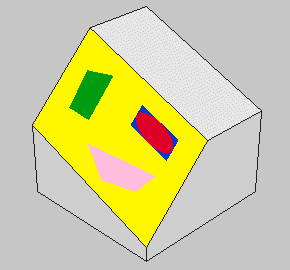 |
1 3 0 0 0 1 0 0 0 1 0 0 0 1 s\3039s01.dat 1 15 0 2 -20 1 0 0 0.4 1 -0.5 0 0 0.5 test_def_1.dat Et maintenant, par "déformation" (un peu moins simple), nous allons plaquer le motif sur la face : Dans ce cas, nous voulons toujours déformer en Y, avec une évolution suivant Z, c'est-à-dire mettre une valeur de -0.5 au 6ème paramètre de la matrice. En plus on veut également déformer en Y, avec une évolution en X, il faut donc changer le 4ème paramètre. Par tâtonnement, pour ne pas trop chercher dans la théorie (moyenne en Y sur les valeurs des points des bords), la valeur 0.4 correspond à notre attente. C'est terminé, le motif est bien placé, et rempli correctement la face. |
Cette méthode à l'avantage de permettre de créer un motif sans avoir la nécessité de le créer avec la face ramené dans un plan de base, et de pouvoir placer ce motif avec des modifications simples de la matrice.
Un inconvénient, est que le motif peut être déformé de façon indésirable, par exemple les cercles
ne sont plus circulaires. Egalement, en cas d'utilisation de primitives dans le motif, on peut voir
apparaître une message "Warning" (Attention) sous LDView :
Part transformed non-uniformly (Elément transformé non-uniformément).
Nous pouvons utiliser la déformation pour mettre un texte crée avec txt2dat en italique. Naturellement les polices de caractères ont généralement une version italique, mais il n'y a qu'une seule valeur d'angle. Avec la "déformation", on peut jouer sur cet angle d'inclinaison.
 |
1 15 0 0 0 1 0 0 0 1 0 0 0 1 test_italique.dat 1 15 0 0 0 1 0 0.8 0 1 0 0 0 1 test_italique.dat 1 15 0 0 0 1 0 1.2 0 1 0 0 0 1 test_italique.dat Dans ces exemples, placés dans le plan XZ, la déformation se fait suivant X, et donc la valeur à changer est la 3ème valeur de la matrice de transformation. Nota : On peut également jouer sur la longueur du texte en changeant la 1ère valeur de la matrice de transformation, et la hauteur sur la 9ème valeur. |
Ce tutoriel est une base de départ pour expérimenter les déformations de primitives. Il suffit souvent d'y penser, lors de la création de pièces LDraw, pour trouver une application qui permet de faciliter cette création, tout en diminuant généralement le nombre de primitives à utiliser.
En conclusion, bonnes expérimentations et bonnes créations.
J.C. Tchang